电脑上纸牌的玩法 微软纸牌如何玩法深度剖析

　　电脑上纸牌的玩法，电脑上纸牌游戏是众多游戏爱好者所钟爱的一种消遣方式，尤其是微软纸牌。微软纸牌是一款集成了多种纸牌游戏的应用，拥有简单易懂的操作、精美的画面以及丰富多样的玩法。无论是在休闲娱乐时还是在繁忙工作中的小憩，微软纸牌能够带给我们无尽的欢乐。下面我们就来深度剖析一下微软纸牌的玩法。

微软纸牌如何玩法深度剖析

5 月 19 日第一次更新：

添加了分隔线，便于阅读；增加了一些图片，便于说明（都是在无聊之余玩纸牌碰巧打出来的牌局，放在教程里正合适）；

2018 年 9 月 13 日第二次更新：

采用知乎自带的分割线；适当修改个别描述；

相信 Windows XP 上面的经典游戏《纸牌》（Klondike）一定会成为很多 80、90 后的童年回忆。是的，纸牌无论是其简单却有趣的玩法，还是在那个还没有什么现代化用户界面设计语言的年代的牌面图案，再加上通关时候那充满动感的动画，无不吸引着一代人。

XP 版本的动画。费尽心血通关之后，顷刻间，仿佛无数的纸牌从上面掉落下来，在屏幕中勾勒着一笔笔优美的弧线。

Win 7 版本的《纸牌》取消了这个动画，而是采用了如下图所示的扑克牌掉下来摔碎的效果，也很漂亮。

而 Win10 版重新恢复了这个动画效果（总共有三种动画，分别是蝴蝶，烟花，以及下图所示的仿 XP 版本的动画效果）。

可是这款游戏，经常玩着玩着就 GameOver 了，甚至有些时候开局无比的顺利，比如四张 A 都露在外面，而且上面牌堆里翻出来的每一张牌都可以拖下来放在下面。可是即便如此，玩到最后还是输了。那么，《纸牌》这款游戏究竟有没有什么窍门，或者规律供我们摸索呢？遇到仿佛失败的情况时，我们有没有什么应对方法呢？答案是肯定的。正如文章的标题所写的那样，我们今天就来聊一聊微软《纸牌》攻略。

读完本文，您将能够：

遵循一定套路，轻松应对 90% 以上牌局辨别牌局是否有解快速设计无解的牌局更高效地欣赏通关动画目录游戏基本规则（20%）牌局难度及是否有解重要概念：牌局通关与隐藏牌堆的关系核心理念：全心全意地翻开隐藏牌（40%）重要概念：分歧点及有目的的撤销（75%）经典技巧：交替上位法（90%）升华：冲击最后的 10%（100%？）总结游戏基本规则（20%）

（标题中的“20%”指的是掌握当前规则后能够应对的牌局占比）

为便于解释，我们进行如上图的命名。这些名词在下文全部位置以斜体进行标注。

（此处我们只讨论标准模式，只翻一张的游戏模式。翻三张以及维加斯式计分方法更为复杂，此处暂不做讨论。）

如上图所示，游戏的基本规则如下：

下方堆叠牌堆按照从上到下从大到小依次递减，且红黑花色交替的方式进行堆叠；空位上只能安放四种花色的 K（除非这张牌是开局即位于空位上，或这张牌是从下方牌堆中翻出来的，例如上图最左边的 ♥10）；右上方的已完成牌堆分别摆放四种花色的牌，其中 A 可以直接放上去，而其他的牌只有比其牌面数值小 1 且花色完全相同的牌在上面时才能放上去；下方有些牌背面朝上放在其他亮出的牌的下方，称为隐藏牌堆。它们只有在其上方的牌移走后才能露出；左上方的随机牌堆中摆放着可供玩家直接操作的纸牌；游戏的通关目标是将所有牌移动到已完成牌堆。

游戏的操作方法有：

拖动到牌面数值大 1 的不同颜色的牌上；拖动到空位上（仅限 K）；拖动到已完成牌堆（按照前面提到的规则进行）；撤销（不限次数）。

好了。看到这里，你应该已经可以解整个游戏大约 20% 的关卡了。这便是章节标题中数字的含义。当然，只是笔者随便估计的数值，认真你就输了。

牌局难度及是否有解

另外，本游戏存在难度之分，而且牌局存在有解和无解的区别。我们先随便聊一聊游戏的难度吧。Win 10 版本提供了总计六种难度（一定有解）供玩家体验。它们分别是：

大致可以翻译为：

简单中等困难专家大师特级大师

知道了上一章节的规则后，基本上简单难度和部分中等难度已经没有什么问题了。

重要概念：牌局通关与隐藏牌堆的关系

请大家牢记一句话：

牌局能否通关等价于下方隐藏牌堆中的牌能否全部翻出。

我们可以这样思考：首先，下方堆叠牌堆的牌都是按照大小顺序排列的，而左上方的随机牌堆的牌全都是可以直接进行操作的。假设除去已完成牌堆，所有的牌都只存在于下方堆叠牌堆和随机牌堆，那么在任何时候，都可以找到合适的牌将其移动至已完成牌堆。是不是这样的一个道理呢？

因此，如果存在至少一张处于隐藏牌堆且其上方牌无法移走的牌，那么本局一定无解。

举个例子吧。其实本文的封面图片就是无解的：

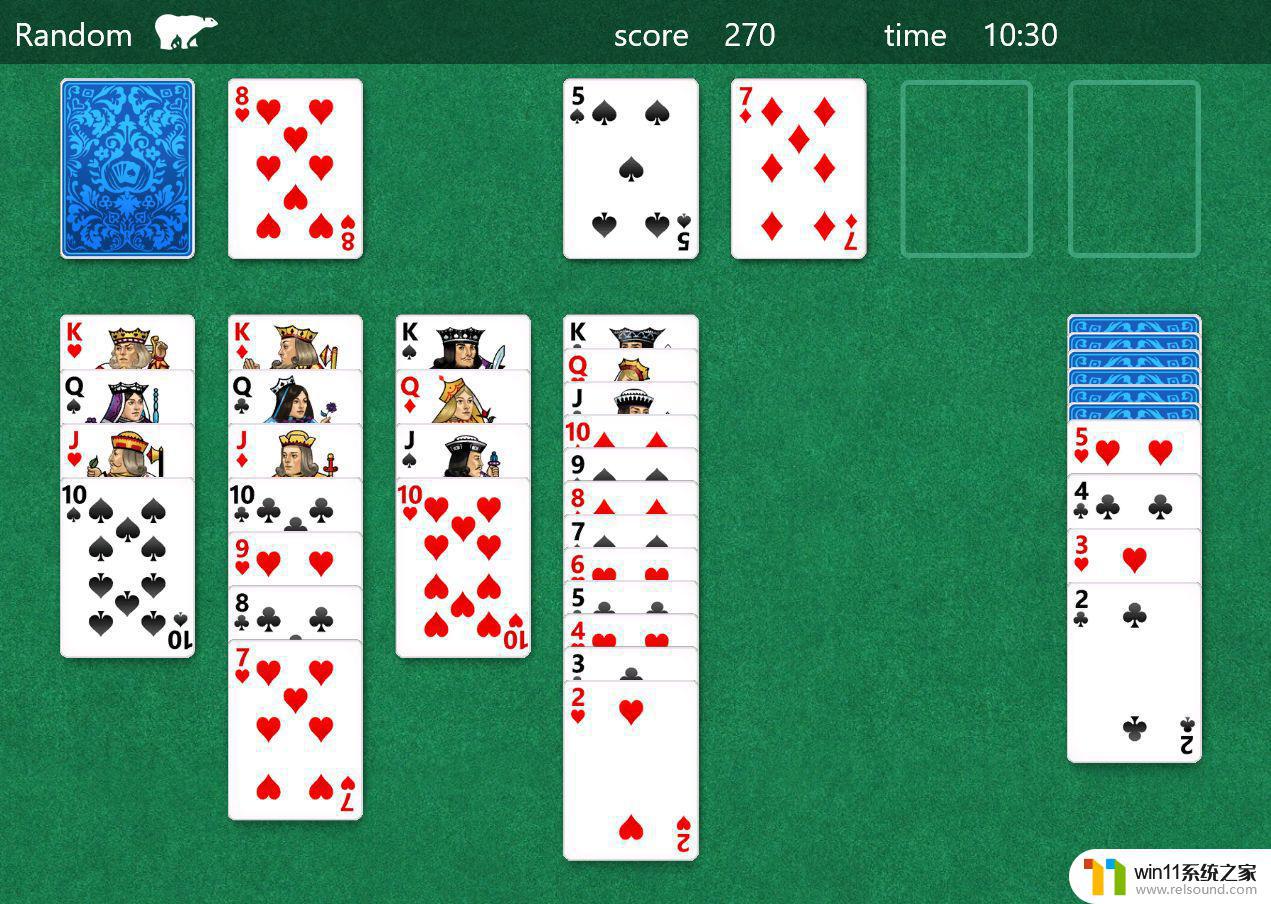
左上方随机牌堆中有：♥8，♠8，以及 ♣7。经过简单计算，隐藏牌堆中有所有（两张）黑色的 6，♦5，以及 ♥A 和 ♣A。这时候，最右侧的隐藏牌堆的牌是一定无法翻出的，因为其上方的 ♥5 无法移开。结合前面说过的操作方法，想要移开 ♥5 只有四种可能：

放到空位上（不可能，因为只有 K 可以）；放到黑色的 6 上（不可能，因为所有黑色的 6 都在这张 5 下方）；拖动到已完成牌堆（不可能，因为 ♥A 在这张 5 下方，所以比 ♥5 小的牌都无法移动上去）；撤销（这个情况较为复杂，我们会在后文进行详细解释。但是这个方法也是没用的，可以暂时简单理解为，另外一张红色的 5 也在隐藏牌堆中，因此不存在分歧点）

因此，本局无解。

我们再来看一个例子：

这一局同样无解。不难发现，随机牌堆已经没有牌了。而目前为止并没有一张黑 8 出现，更不幸的是 ♦4 也在右侧 ♦7 下方，所以这张 7 绝对无法移走。所以无解。（打出无解的牌局并截图还真是挺费功夫的）

同时，我们也可以得到这样的一个启发：如何快速而且有效地设计一个无解的纸牌牌局？

答案一：设计一张 ♥5，可以在下方任意位置，甚至在隐藏牌堆中，然后其下方（压住）有所有黑色的 6，从而保证这张 5 不可能移动到别处。同时，比 ♥5 小的同花色的牌的任意至少一张也在这张 5 下面压着，那么这次牌局无论前面有多么顺利，都不可能赢。

答案二：设计一张 ♠Q，下面只压着 ♠J 和两张红 K。好了，这个牌局能把玩家气死。因为四种花色的 1~10 全都能移动到已完成牌堆，然而还是输了。

答案三：设计两张红 7，分居不同的两列。他们俩下方压着两张黑 8 和两张红 6。

答案四：设计两张 ♥7 和 ♥8，分居不同的两列。他们俩下方压着所有的黑 7 和黑 8，以及 ♥6。

……

（5 月 19 日新增）

上图就是一种典型到不能再典型的无解局。大家可以看到，除了那三张牌，其他全部已经亮出。看似顺利无比，可依旧必输无疑。原因也请大家结合我之前的讲解进行分析，相信对于现在的大家来说这一定非常简单。

总而言之，只要有那么一张牌，无论如何都移不开，其下方的隐藏牌堆永远暗无天日，那么这局一定无解。当然大家肯定也能够明白，我并不是在教大家怎样设计无解的牌局，而是在教大家怎样快速判断当前牌局是否有解。通过观察与统计随机牌堆与下方堆叠牌堆的所有牌，不难算出隐藏牌堆里都有些什么牌，特别是在全盘只有一到两列隐藏牌堆没有翻开的时候。一旦判断是无解局，那么请立刻放弃吧，不要再浪费时间了。

核心理念：全心全意地翻开隐藏牌（40%）

回到上一章节开头的那句话：任意牌局能否通关等价于下方隐藏牌堆中的牌能否全部翻出。因此，玩这款游戏过程中的核心理念其实就是一句话：力所能及地去翻开下方所有在隐藏牌堆中的牌。

隐藏牌堆上方有一张 K，但是没有空位（可能是随机牌堆中移下来了一张 K 占用了空位）；隐藏牌堆上方有一张黑 5，但是黑 5 不能移动到别处的红 6 上，因为别处唯一一张可用的红 6 被另外一张黑 5 占用（可能是随机牌堆中移下来了一张黑 5 占用了红 6）；隐藏牌堆上方有一张黑 5，但是黑 5 不能移动到右上的已完成牌堆，因为这张黑 5 上方压着一张红 4，而别处没有其他的可用黑 5，所以无法移开（可能是随机牌堆中移下来了一张红 4 妨碍了黑 5）。

从括号中的内容不难发现，很多时候随机牌堆中移下来的牌帮了倒忙。综上所述，我们制定这样一条原则：只有确定能够产生意义的情况下，才将随机牌堆中的牌拖动到下方。这样的移动叫做有效移牌，反之为无效移牌。例如：

这时，下方的牌堆是没有牌能够移动的。如果将这张黑色的 Q 移动至下方红色的 K 上，则能够使 ♦J 移动，从而亮出下面的牌。这是一次有意义的移牌，所以是有效移牌。

那么这个呢？要不要将这张红色的 4 移动下来呢？因为现阶段将其移动下来并不能产生意义，即这（可能）是一次无效移牌，所以我们先不这样做。为什么说“可能”呢？是因为下方隐藏牌堆中可能会出现一张黑色的 3，在这种情况下，这张红 4 就变得有意义了。不过我们不要仅因为存在这样的可能性，就轻易操作每一次无效移牌。因为这有可能导致将来 ♣5 因为这张 4 压着，而无法移动到已完成牌堆，或别处隐藏牌堆中新亮出一张红 4，却因为下方唯一的黑 5 被这张“不速之客”占用，而无法亮出其下方的牌。

这张红 8 要不要移动下来呢？

遇到这种情况，一般可以无脑将红 8 移动下来。因为这里，两张黑 9 全部亮了出来，所以很难遇到前面说的那些问题。同时这张红 8 或许还可以在将来让下方的黑 5 移动至其上方（黑 7，红 6，黑 5），从而产生意义。

另外还有一件值得注意的事情：这两张黑 9 下方均为隐藏牌堆或空位，所以这两张牌都是本来就在下方的。这有什么值得注意的呢？我们假设这时出现一张红 10 放在了下方左侧黑 J 上，那么该移动哪张黑 9 上去从而亮出底牌呢？这就涉及到了下一章我们将要重点讲解的分歧点了。简而言之，左侧的黑 9 可能给你带来空位，从而使别处的 K 移动到空位上。而右侧的黑 9 下方压着大量的隐藏牌，如果不移开，可能后患无穷。究竟该如何考虑？我们稍后再进行分析。

明确游戏规则理解什么情况会导致游戏伪失败明白游戏存在无解的情况懂得只操作有效移牌

好了，看到这里，应该已经可以轻松玩通简单和中等两个难度了，大约占全部游戏的 40%。接下来的内容可能会变得有些不好理解，但是我相信聪明的读者朋友们一定可以看明白的。

重要概念：分歧点及有目的的撤销（75%）

（请注意，如果您玩的版本不支持无限制撤销，如 XP 版，那么可以考虑不看剩下的内容，因为下文全部基于可无限制撤销的模式）

看到标题可能有人会问了：老师，这又不是文字冒险游戏，哪来的什么分歧点啊？

哈哈，我可以告诉你，分歧点才是这款游戏的魅力所在，也正是难倒了绝大多数新手玩家的罪魁祸首！

那么，什么是分歧点呢？说白了，分歧点就是有两张同样牌面数值，且颜色相同但花色不同的牌（如 ♠5 和 ♣5），而当前只有一张红 6 可用，那么这便是一个分歧点。还有另外一种分歧点，比如现在只有一个空位，但是有两个 K 都可以放在上面，那么这也是一个分歧点（这个是随意花色的，要求没有第一种分歧点那么严苛）。之所以说它是分歧，是因为你的选择有可能直接导致牌局走向胜利，或进入伪失败。

很好。然后，我们再来复习一个重要概念。或者说游戏规则：如果一张牌的下方是隐藏牌堆或这张牌不是 K 却位于空位上，那么这张牌一定来自下方，而非随机牌堆（空位上的 K 分情况，比如一张 K 正好是隐藏牌堆的最后一张牌，那么它就是在空位上且来自下方的 K。为使行文简洁，不做赘述）。我相信这条概念对于大家来说不难理解。

好了，现在我来教大家一条特别重要而且有效的技巧：有目的的撤销。具体而言，就是根据目前伪失败的局面，分析可能造成失败的分歧点，然后撤销到那一步。通常情况下，新手遇到伪失败的情况，可能会意识到撤销有时会带来意外的惊喜，但是并不能够分析出具体撤销到哪一步才合适。所以，这里重点强调「有目的」三个字。

看文字实在是晦涩难懂，难以想象出实际情况。我们来看牌局吧。

这里，已经伪失败了，随机牌堆不能产生任何有效移牌。分析原因，可以看到两张红 5 下方是空位或隐藏牌堆，所以两张红 5 都来自下方，不存在分歧。右侧 ♦2 也不存在分歧，因为目前为止并没有出现黑 3，且只有这一张红 2 露出。也不会是左侧 ♠J，同理，目前只有这一个黑 J 出现。

但是！右侧的 ♠5 却有可能是因为左侧 ♣5（可能来自随机牌堆或下方）占用了唯一的红 6 而无法移动。因此，当初选择这两张黑 5 的时刻就是一个分歧点。

所以，找到了原因之后，我们撤销至 ♣5 放到红 6 前的位置。

好的。这里可以看到，♣5 也是来自下方的牌堆，而不是从随机牌堆来的不速之客。我们现在把 ♠5 移动到右侧红 6 上面，然后继续玩……

结果却再次遭遇伪失败。因为我们已经尝试了将两个黑 5 产生的两个分歧路线，却都遭遇了伪失败，因此罪魁祸首已经不是黑 5 了。请大家根据我之前的讲解，分析这次的罪魁祸首是什么？

其实这里分歧点有很多，但是我们这里讲解的重点不是如何通关当前牌局，而是教会给大家一个「通解」，从而使大家能够快速有效地找到产生分歧点的牌。希望大家多次阅读上面的内容，并加以思考，从而彻底理解分歧点的含义。

答案是红 10。大家答对了吗？（回答红 6 也是正确的，不过我们这里暂时只关注红 10 的分歧）

如果我们当初不将 ♥10 移动到左侧黑 J 上方，而是将 ♦10 移动上去，那么我们将得到一个空位，从而将下方的 K 移动到空位上。

所以，我们继续撤销，直到 ♥10 离开黑 J。

好。现在，我们将 ♦10 移动到黑 J 上，然后继续游戏。

最终，我们迎来了游戏胜利。

同时，有些时候会出现不止一个分歧点的情况。那么，在这种情况下，我们不妨先撤销到最近的一次分歧点，并尝试另一种方法继续进行游戏。如果发现并不能通关（这并不能表示该处分歧点对游戏胜负不产生影响），就再进行撤销，直到另外一个分歧点。从较早的分歧点出发，可能会再次遇到类似我们第一次撤销到的分歧点（虽然整个局势已经发生了变化）。这时候，就需要我们通过良好的思考能力与记忆能力，分析出各个分歧点之间的关系，从而将游戏继续玩下去，直到通关。游戏的难度其实就是极大程度的和这些分歧点互相之间的关系挂钩的。关系越复杂，难度就越高。

怎么样？是不是很简单呢？

所以，在前面的章节中我们问的那个问题，遇到分歧点，究竟应该移动哪张牌呢？很遗憾，并没有任何规律。我们只能够根据当前牌局的情况，以及自己的经验进行选择。

不过，理解了分歧点和有目的的撤销后，我们就可以随便选一条路走下去，如果发现是死路就拐回来（类似深度优先搜索）。甚至完全可以理解为，我们得知了未来发生的情况，然后穿越回过去，纠正了自己的错误。我们不断地穿越，不断地纠正，最终走向胜利。假设我们发现了分歧点并撤销回到了游戏刚开始的位置，那么我们就仿佛被"剧透"了「将来可能会发生怎样的分歧」，或者「究竟有哪些牌会在将来捣乱」。知道了这些后续剧情的我们，在考虑很多问题上就会有了答案，比如是否需要将一张无效移牌的随机牌从上面拿下来。

学会了分歧点这一技巧，你已经可以解 75% 的牌局了。困难难度相信早已经易如反掌，甚至专家级的牌局也可以游刃有余了。

经典技巧：交替上位（90%）

看到括号里面的数字了吗？没错，理解了前面说的分歧点后，再加上这个经典技巧，就可以解 90% 的牌局，即特级大师之前的所有难度基本上都可以迎刃而解。

我们来看这样一个牌局（又花了我半天时间截图）：

这里，随机牌堆中只剩一张 ♣10。哎呀，是不是伪失败，甚至无解了呢？因为右侧的 ♥9 并没有办法移到别处的黑 10 上面。同时， ♥2 也在其下方压着，从而没有办法将比 9 小的所有 ♥ 都移动到上方。

不过，相信理解了分歧点的你，不难发现，这里有一张 ♦9 占用了唯一可用的黑 10。所以，我们要不要撤销到那一步呢？

不必。

此时我们就要借助本章节提出的交替上位法。虽然我们没有 ♥2，但是我们有 ♦2，而且不难发现，♦ 的所有比 9 小的牌都在下面。所以，接下来我们要做的是一系列交替移牌操作，可能不太好理解，我会用连续图片进行辅助说明。相信已经看到这里的你，不会在乎这点流量的。

将 ♥4 移动到 ♣5，然后将 ♠5 移到已完成牌堆（这一步骤以下简称上位）。

将左边的 ♣5 移动到 ♥6，然后将 ♦6 上位。

将 ♥5 移动到 ♣6，然后将 ♠6 上位。同时，♠7 上位，♦7 和 ♦8 上位。

将 ♥7 移动到 ♣8，然后 ♠8 上位。同时，♠9 上位。

激动人心的时刻到了：此时，♦9 可以上位了！于是，我们终于可以将右侧的 ♥9 移动到黑 10 上面，亮出底牌。

游戏通关！

那么关键问题是，在什么情况下，交替上位法是有效的呢？其实规律很简单。假设说卡位的牌是 ♠8，那么如果有任意两种颜色不同的花色的（如 ♣ 和 ♦）所有小于等于 8 的牌都在下方，则有很大概率可以使用交替上位法。就上图而言，想要移开 ♠8，那么如果当前局面是 ♣8 占用了唯一的一个红 9，而且 ♣ 以及任意一个红色花色的牌的所有小于等于 8 的牌都可用，那么你将有很大的机会可以使用交替上位法。

但是，如果你不遵守之前提到的核心理念，即你先前制造了多次无效移牌，结果严重阻碍了你使用交替上位法。这种情况下，玩到最后，如果发现是伪失败，那么就请根据分歧点，尽情撤销吧。

是不是可以理解为，交替上位法只是为了节省时间，不用撤销至很久很久以前呢？其实不一定。虽然从上面的例子来看，确实是这么一个故事，但是在某些特殊的情况下，即便撤销也是无济于事的。需要冷静地分析交替上位法是否有效。因为有些时候，一张牌的上位，直接就能够使其下方的隐藏牌亮出来，为牌局带来重大转机。比如下例：

随机牌堆只有一张 ♣10。右侧 ♥J 卡位，而且下方只有这一张红 J，且没有黑 Q。但是不难发现，♣ 和 ♥ 的所有小于等于 J 的牌都是可用的，因此可以借助交替上位法完成此牌局。

好啦。读到这里，并经过适当的练习，再结合自己的思考，相信你已经可以解 90% 的牌局了。

升华：冲击最后的 10%（100%？）

老师，能不能再给力点，采用一些套路轻易解决所有有解的牌局？

这里举一个我曾经花了四五十分钟才完成的牌局为例子。

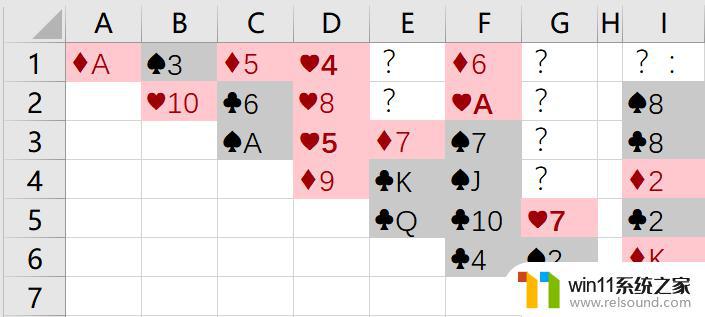
经过多次分歧点搜索，发现当前的牌局是这么一个情况。两张红 7 成为本局最大的难点，因为两张黑 8 都在其下方。问号处的牌为右侧列举的六张，具体位置不明。

分析过程如下：

经过多次调换次序，玩到后面会发现有两张红 7 卡位（E、G 列）可得两张红 7 压着的牌（即 6 个？位）如右侧所列，所有黑 8 都在？中所以必须将至少一种红色牌的 1~6 全部上牌，从而使红 7 下面的牌翻出♦2 在？中，所以只能上 ♥1~6♥A（F 列）在很下面，其上的 ♣4 因为 ♣2 在？处所以不能放在 ♥5 上面，否则 ♥5 上不去这时候需要额外的黑 6 以及 ♦7 的帮助但是 ♦7 上面有黑 KQ，所以至少需要两个空位才能移开这两张牌（现有的只有一个黑 K，没有帮助），从而 ♥A 这边的黑J也可以放在黑 K 上面于是，F 列 ♦6 可以放在黑 7 上，D 列 ♥4 也可以放在 ♦6 上，因为有空闲的红 8 在下面（D 列）终于，一个渐渐瓦解 D、F 列的计划诞生了。F 列的 ♣4 需要 C 列 ♦5 的帮助，而 C 列 ♣6 不能放在 ♥7 上面，所以还需要 E 列 ♦7 的帮助。因此有了空位，应尽早考虑移动 E 列的 K……

我已经不知道我在写些什么了。纸牌的牌局无限灵活，但是有解的牌局，一定是可以找到方法来通关的。鄙人才疏学浅，暂时并没有找到有效的攻克最后 10% 的方法。希望日后我能够灵光一现，或者仰仗诸位读者朋友寻找到更棒的解法。

总结

本文详细介绍了：

纸牌的游戏规则有解和无解的情况什么是“伪失败”牌局通关与隐藏牌堆的关系核心理念：一切为了翻开隐藏牌重要概念：分歧点经典技巧：交替上位

希望所有喜欢这款经典纸牌游戏的朋友们能够得到启发。

电脑上的纸牌玩法丰富多彩，不仅能够娱乐消遣，还能够锻炼我们的思维和逻辑能力。微软纸牌作为一款经典的纸牌游戏，其简单易学、玩法多样的特点深受广大玩家的喜爱。希望大家能够在这款游戏中找到乐趣、享受快乐，进一步提高自己的游戏水平。